último tiempodiscutimos esto, lamentablemente, segúnStatu quo de CSS 2025 Las encuestas muestran que las funciones trigonométricas se consideran las características CSS «más molestas».

Esto me sorprendió. Como un nerd de las matemáticas, podría incluso sentirme un poco ofendido. Entonces escribí un artículo tratando de mostrar cómo usarcos()ysin() Función. Hoy quiero explorar otra: la función tangente, tan().

Antes de dar un ejemplo, debemos preguntarnos ¿qué es?tan() ¿primero?

definición matemática

La forma más sencilla de definir tangente Ángulo significa igual al seno dividido por coseno.

Nuevamente, esta es una definición bastante simple y no nos da mucha idea de qué es la tangente o cómo usarla en su trabajo con CSS. Ahora, por favor recuerdatan()De la división de ángulos funcionales que comentamos en el primer artículo.

a diferencia decos()ysin()emparejado con muchos círculos,tan()Más útil cuando se trabaja con triángulos, especialmente un triángulo rectángulo, lo que significa que tiene un ángulo de 90°:

Si elegimos uno de los ángulos (en este caso el ángulo inferior derecho), tenemos un total de tres lados:

• este cercano Un lado (el lado del ángulo de contacto)
• este Opuesto Un lado (el lado alejado del ángulo)
• este hipotenusa (lado más largo)

Desde estas perspectivas,tan()El cociente de un ángulo es la división de los lados opuestos y adyacentes de un triángulo:

Si la otra parte crece, el valortan()Aumentar. Si los bordes adyacentes crecen, entoncestan()reducir. Arrastra las esquinas del triángulo en la demostración a continuación para estirar la forma vertical u horizontalmente y ver cómo cambian los valores.tan()Cambie en consecuencia.

Ahora podemos empezar a ver cómo utilizartan()Funciones en CSS. Creo que una buena forma de empezar es mirar un ejemplo de cómo organizar una serie de triángulos en otra forma.

Lista segmentada

Imaginemos que tenemos una lista desordenada de elementos y queremos organizarlos en algún tipo de polígono, donde cada elemento es untriangularRebanadas de pastel poligonal.

Entonces, dondetan()¿Funciona? Comencemos con nuestra configuración. Como la última vez, tenemos una lista diaria desordenada de elementos de lista indexados en HTML:

<ul style="--total: 8">
  <li style="--i: 1">1</li>
  <li style="--i: 2">2</li>
  <li style="--i: 3">3</li>
  <li style="--i: 4">4</li>
  <li style="--i: 5">5</li>
  <li style="--i: 6">6</li>
  <li style="--i: 7">7</li>
  <li style="--i: 8">8</li>
</ul>

notas:Este paso se convertirámuchocuandosibling-index()ysibling-count()La función es compatible (yellos sonrealLimpio). Mientras tanto, estoy codificando el índice usando variables CSS en línea.

Entonces, tenemos --total Cantidad de artículos (8) y valor del índice (--i) para cada proyecto. Definiremos el radio del polígono, que puedes considerar como alto Para cada triángulo:

:root {
  --radius: 35vmin;
}

Simplemente agregue un poco de estilo a la lista desordenada para convertirla en un contenedor de cuadrícula, colocando todos los elementos exactamente en su centro:

ul {
  display: grid;
  place-items: center;
}

li {
  position: absolute;
}

Ahora podemos cambiar el tamaño del elemento. Específicamente, configuraremos el contenedor width a dos veces--radius variables, y cada elemento es un--radiusancho.

ul {
  /* same as before */
  display: grid;
  place-items: center;
  /* width equal to two times the --radius */
  width: calc(var(--radius) * 2);
  /* maintain a 1:1 aspect ratio to form a perfect square */
  aspect-ratio: 1;
}

li {
  /* same as before */
  position: absolute;
  /* each triangle is sized by the --radius variable */
  width: var(--radius);
}

Hasta ahora nada. Tenemos un contenedor cuadrado con ocho elementos rectangulares apilados uno encima del otro. Esto significa que solo vemos el último elemento de la serie, ya que el resto está oculto debajo de él.

Queremos colocar el elemento alrededor del punto central del contenedor. Tenemos que rotar cada elemento uniformemente en un cierto ángulo, que podemos obtener dividiendo un círculo completo,360degsegún el número total de elementos, --total: 8luego multiplique ese valor por el valor del índice en línea de cada elemento, --ien HTML.

li {
  /* rotation equal to a full circle divided total items times item index */
  --rotation: calc(360deg / var(--total) * var(--i));
  /* rotate each item by that amount */
  transform: rotate(var(--rotation));
}

Pero tenga en cuenta que estos elementos aún se cubren entre sí. Para resolver este problema, trasladamos sutransform-originllegarleft center. Esto mueve todos los elementos un poco hacia la izquierda al girar, por lo que tenemos que trasladarlos hasta la mitad del camino hacia el centro.--radiusantes de realizar un giro.

li {
  transform: translateX(calc(var(--radius) / 2)) rotate(var(--rotation));
  transform-origin: left center;

  /* Not this: */
  /* transform: rotate(var(--rotation)) translateX(calc(var(--radius) / 2)); */
}

Esto nos da una forma de rayos de sol, pero está lejos de ser un verdadero polígono. Lo primero que podemos hacer es utilizarclip-pathpropiedad:

li {
  /* ... */
  clip-path: polygon(100% 0, 0 50%, 100% 100%);
}

un poco como rueda de la fortuna Pero hay lagunas entre cada panel:

Queremos cerrar estas brechas. Lo siguiente que debemos hacer es aumentar la altura de cada elemento para que sus lados se toquen, formando un polígono perfecto. ¿Pero por cuánto? Si jugamos con números concretos, podemos decir que para un octágono, cada elemento del mismo es200pxde ancho, la altura perfecta del artículo es166pxAlto:

li {
  width: 200px;
  height: 166px;
}

Pero ¿y si nuestros valores cambian? Tenemos que calcular manualmente la nueva altura, lo cual no es bueno para el mantenimiento. En su lugar, usaremos lo que espero que se convierta en su nueva función CSS favorita para calcular la altura perfecta para cada elemento.tan().

Creo que sería más fácil ver cómo se vería esto si lo redujéramos un poco y creáramos un cuadrado simple con cuatro elementos en lugar de ocho.

Ten en cuenta que puedes pensar en cada triángulo como un par de dos triángulos rectángulos presionados uno contra el otro. Esto es importante porque sabemos tan() Muy, muy bueno usando ángulos rectos.

Bueno, si sabemos a qué equivale el ángulo cerca del centro, entonces podemos encontrar la longitud del lado opuesto (alto) del triángulo usando la longitud del lado adyacente (ancho).

¡Conocemos el ángulo! Si cada uno de los cuatro triángulos del recipiente se puede dividir en dos triángulos rectángulos, entonces sabemos que los ocho ángulos totales deben equivaler a un círculo completo, que mide 360°. Dividiendo todo el círculo por el número de ángulos rectos obtenemos 45° para cada ángulo.

De vuelta a nuestro polígono general, lo convertimos a CSS así:

li {
  /* get the angle of each bisected triangle */
  --theta: calc(360deg / 2 / var(--total));
  /* use the tan() of that value to calculate perfect triangle height */
  height: calc(2 * var(--radius) * tan(var(--theta)));
}

Ahora, no importa cuál sea el radio del contenedor o cuántos elementos contenga, ¡siempre tendremos el valor de altura perfecto para el triángulo!

Echa un vistazo a esto. podemos jugartransform-origin¡Valores de propiedades para obtener diferentes tipos de formas!

Esto se ve genial, pero realmente podemos usarlo. Convirtamos esto en un menú radial donde cada elemento es una opción entre la que puedes elegir. La primera idea que me vino a la mente fue algún tipo de selector de personajes, algo así como la rueda de personajes en Grand Theft Auto V:

…pero usemos más, digamos, personajes abrazables:

Quizás hayas notado que me puse un poco elegante y corté todo el recipiente en forma redonda usando clip-path: circle(50% at 50% 50%). Cada elemento sigue siendo un triángulo con lados duros, pero recortamos el recipiente que contiene todos los elementos, dándoles una forma redondeada.

Podemos usar exactamente la misma idea para hacer una galería de imágenes poligonal:

Este concepto probablemente funcione el 99% de las veces. Eso es porque las matemáticas son siempre las mismas. Tenemos un triángulo rectángulo y conocemos (1) el ángulo y (2) la longitud de uno de los lados.

tan() en la naturaleza

he visto tan()Esta función se utiliza en muchas otras demostraciones excelentes. ¿Adivina qué? Todos se basan exactamente en las mismas ideas que vemos aquí. Échales un vistazo porque son increíbles:

• Nils Binder tiene este gran diseño diagonal.
• Slajana Stojanovic Diseño de rompecabezas Tangram Utiliza el concepto de tangentes.
• Temani Afif usa triángulos en un montónpatrones CSS.
• De hecho, Temani es una gran fuente de ejemplos de funciones trigonométricas. verás tan() Destacado en muchas de las cosas que hizo, como forma de floromigas de pan modernas.

Bonificación: tangentes dentro del círculo unitario

En el primer post hablé mucho de círculo unitario: Un círculo con un radio de una unidad:

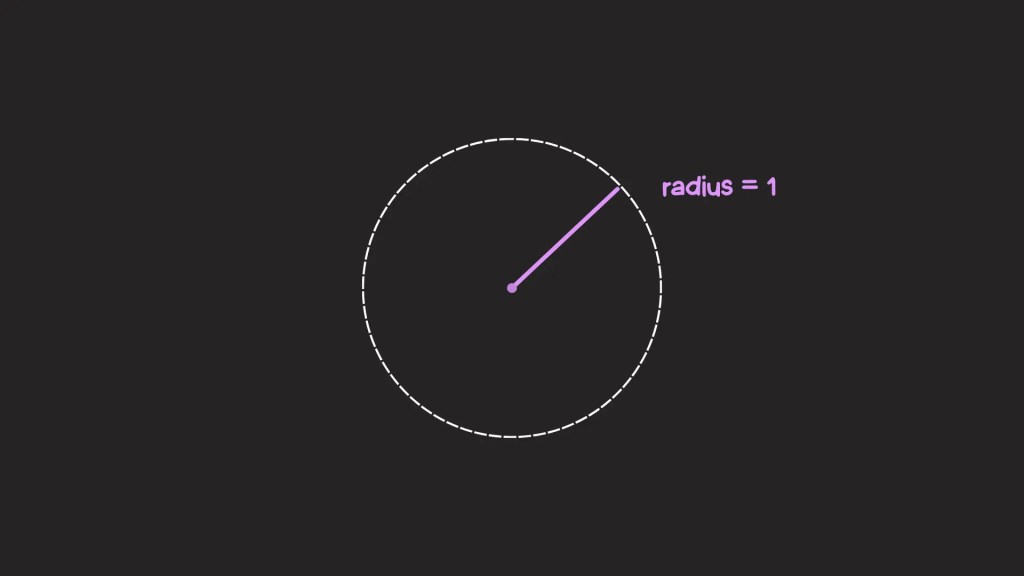
Podemos mover la línea del radio en un ángulo alrededor del círculo en sentido contrario a las agujas del reloj, lo que se demuestra en este ejemplo interactivo:

También mostramos cómo, dado el ángulocos()ysin()Las funciones devuelven las coordenadas X e Y de los puntos finales de la línea recta en el círculo respectivamente:

Ahora sabemos que la tangente está relacionada con el seno y el coseno gracias a la ecuación utilizada para calcularla en el ejemplo que vimos juntos. Así que agreguemos otra línea a nuestra demostración para decir tan() valor.

Si tenemos un ángulo, entonces podemos proyectar una línea (llamémosla L) comenzando desde el centro, su punta caerá en algún lugar del círculo unitario. Desde allí, podemos trazar otra línea perpendicular a L A partir de este punto, trabaje hacia afuera a lo largo del eje X.

Después de experimentar con ángulos, es posible que notes dos cosas:

1. este tan()Los valores son positivos sólo en los cuadrantes superior derecho e inferior izquierdo. Si te fijas en los siguientes valores entenderás por quécos()ysin()Allí, ya que están separados unos de otros.
2. este tan()Los valores a 90° y 270° no están definidos. ¿Qué queremos decir con no claro? Esto significa que el ángulo crea una línea paralela infinitamente larga a lo largo del eje X. Decimos que es indefinido porque puede ser infinito hacia la derecha (positivo) o hacia la izquierda (negativo). Ambos son posibles, por eso decimos que no está definido. Como no tenemos «indefinido» en el sentido matemático de CSS, debería devolver un número excesivamente grande, dependiendo de la situación.

¡Más trigonometría por venir!

Hasta ahora hemos cubiertosin() cos()ytan()funciones en CSS y (con suerte) demostramos con éxito su utilidad en CSS. Aún así, nos perdimosBizarroEl mundo de las funciones trigonométricas:asin(),acos(),atan() atan2().

Esta es la característica CSS «más molesta» que discutiremos en la tercera y última parte de esta serie.

---

La función CSS «más molesta»: tan() Publicado originalmente en Consejos CSS,Esto es océano digital familia. debería Recibe el boletín.